TL;DR

这篇论文首先是引入了 relaxed monotonicity 的概念，然后基于对向量索引的 relaxed monotonicity 性质的观察：ANN 的检索过程中会有两个阶段，第一阶段中会快速向目标向量靠近，第二阶段向量整体上会逐渐远离目标向量。论文中给出了判定查询已经进入第二阶段的方法，因此可以在判定进入第二阶段后，且已获得 $k$ 条结果后提前结束查询，从而优化性能。

但这个性质强大的地方在于，只要我们知道检索过程已经进入第二阶段，意味着从此刻开始，我们可以继续查询以取得更多向量，且结果整体上是距离升序的。因此可以摆脱传统 ANN 算法的 TopK 查询模式，实现流式的结果输出。

在流式的原语下，标量过滤，混合打分，多向量查询，甚至向量 join 等功能都可以实现很大幅度的性能提升。

松弛单调性（Relaxed Monotonicity）

从单调性的角度去看索引，索引内部其实是从一个点开始，不断查找数据，并且每次迭代中都越来越接近目标值。而向量索引不具备严格的一致性性质，以论文中的图例中的 HNSW 为例：

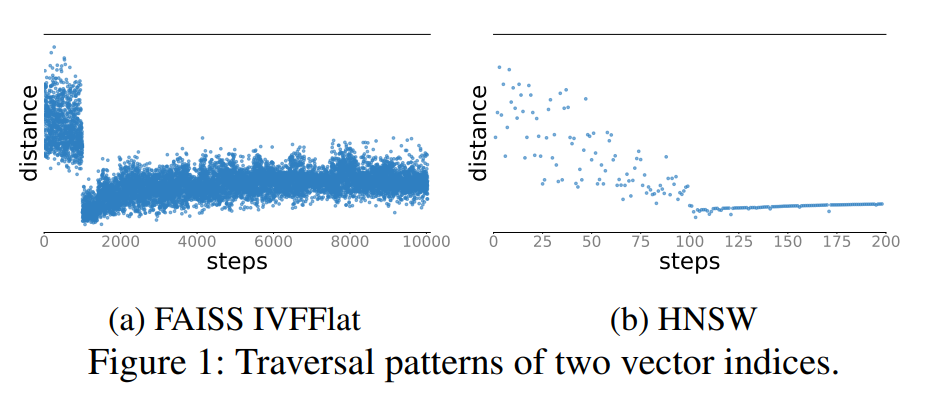
从图中可以看出，向量索引的查询过程可以分为两个阶段。查询前期是在上层图中做遍历，候选集中的结果会快速接近目标值，但当算法不断执行，到后期时，候选集就已经收敛了，继续遍历时很难得到更优的结果。

如果我们能够判定这个拐点，则可以优化 ANN 算法：在进入第二阶段后，获取 $K$ 条结果后就可以停止搜索。论文中给出了方法：

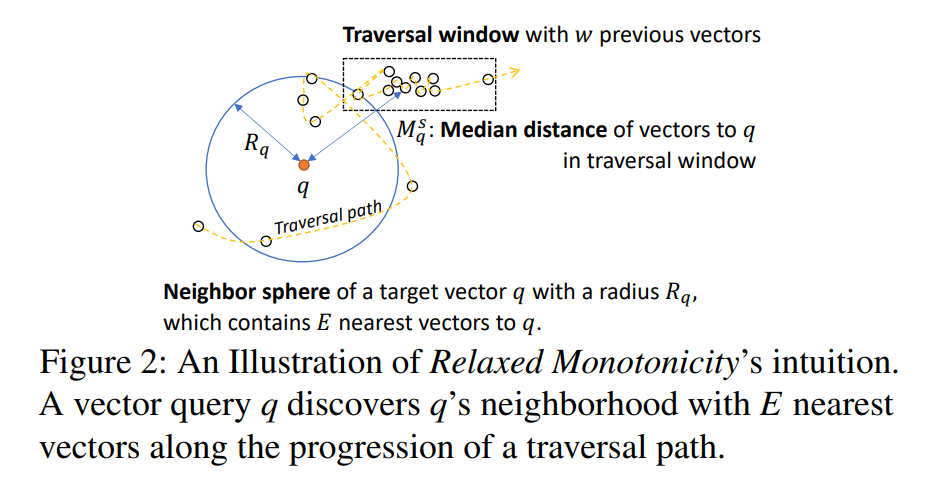
其中 $q$ 为目标向量，$R_q$ 为邻点集半径，$M_q^s$ 为当前 traversal window 到 $q$ 的距离中值。 这个图示给出了一个直觉上的判断方法：只要 $M_q^s \geq R_q$，那么查询就可能已经进入了第二阶段。

需要注意这并不是一个严谨的结论，考虑图示，如果是查询 Top2 且 $w=1$，那么上面的方法会判定此时已经进入了第二阶段，但此时 recall 为 0。实际实现中，以 HNSW 为例，在 coarse-grained graph 中不使用上面的方法进行判定，而是总是搜索，到 fine-grained graph 中再使用上面的方法进行判定。还可以选取更大的 $w$ 值来提升 recall。

Relaxed monotonicity 提供了一种一种强大的原语：算法只需要执行到进入第二阶段时，就可以停止，保存此时查询过程中的状态，就可以不断产出结果，也就是可以提供流式的查询原语。

场景优化

利用 relaxed monotonicity 实现的流式查询原语在多种场景下都会显著提升性能。

标量过滤 + 向量查询

带标量过滤的向量查询是目前向量数据库的一个基本能力，受限于 ANN 索引只提供 TopK 的批式接口，目前的向量数据库对这一功能主要有两种实现：

• pre-filtering：先执行标量过滤，标量过滤生成一个 bitmap，之后执行向量查询时用 bitmap 过滤掉数据
• post-filtering：选取一个 $K' > K$，执行向量查询，然后再在结果集上执行过滤

与直觉相反，pre-filtering 会导致 ANN 索引的性能下降，因为可能会需要遍历更多的向量以找到满足数量的结果，通常来说命中率越低，性能也会越差。而 post-filtering 的问题也显而易见，首先 $K'$ 的值并不好选取，因为无法预知会过滤掉多少数据，如果最终结果集不足，可能还需要尝试更大的 $K'' > K'$，性能也会很差。

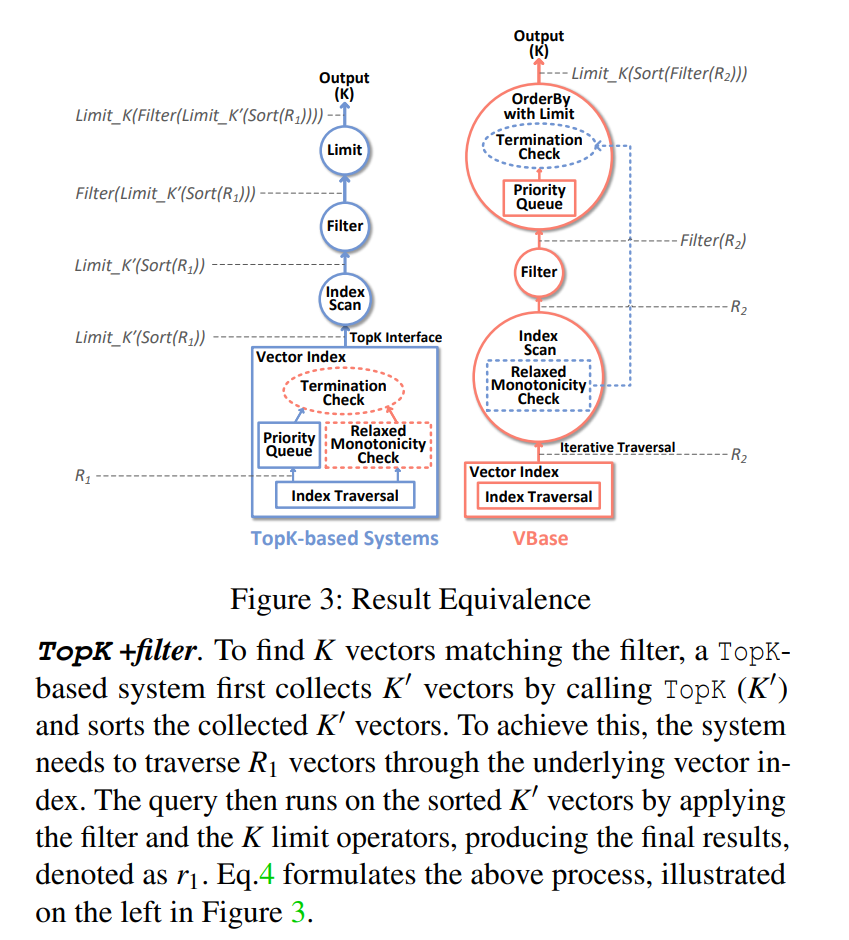
回到标量过滤 + 向量查询的场景，有了流式查询原语后，我们可以不断从索引中取出数据并进行过滤，当最终结果集达到 $K$ 条后，就终止查询。性能上，等价于 post-filtering 在最优 $\widetilde{K}$ 下进行查询。

多向量查询

多向量查询指对多个向量列进行查询并对结果进行聚合，选择聚合后的 TopK 结果。

// 写不下去了，先学一下 NRA 再继续